Determining a Parabola with a Vertex and Y-Intercept

Published 12 March, 2009; last updated on 15 March, 2019; originally posted at blog.craiga.id.au.

So I needed to figure how to come up with a formula for the following graph, given the vertex (i.e. the “turning point”) and the y-intercept.

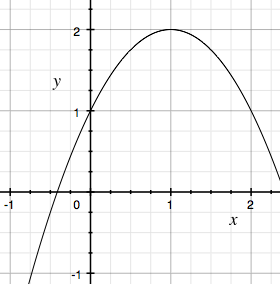
parabola with y-intercept at 1 and vertex at (1, 2)

I remembered the polynomial form from high school, but that only gave me direct control over the y-intercept, and I was able to find the vertex form formula on Wikipedia which gave me the ability to specify a vertex, but gave me no control over the y-intercept. So, after stretching my brain a bit to remember my high school maths, I came up with the following formula:

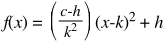
f(x) = ((c-h)/(k^2))((x-k)^2)+h

  • h and k are the x and y coordinates of the vertex
  • c is the y-intercept

So, in the above example, we substituted h and k for 1 and 2 (the coordinates of the vertex), and c for 1 (the y-intercept).